函数y=√(5x-√7x)的图像示意图画法,本经验主要介绍函数y=√5x-√7x的定义域、单调性、凸凹性和极限等性质，并通过导数知识解析函数的单调区间和凸凹区间，同时简要画出函数的示意图。

函数y=√(4+x)+√(5+x)的图像,本经验主要介绍函数的定义域、单调性、凸凹性、极限等性质，并通过函数导数工具解析函数y=√4+x+√5+x的单调性和凸凹性，简要画出函数的图像示意图。

隐函数75x²+61y²+35z²=8的一阶和二阶导数,本文通过全微分法、直接求导、构造函数求导以及多元函数求导法则，介绍计算隐函数75x²+61y²+35z²=8的一阶和二阶导数的过程和主要步骤。

导数画曲线方程2y^2-4xy+9=0的图像示意图,本经验通过函数的定义域、单调性、凸凹性等性质，介绍函数用导数工具画隐函数2y^2-4xy+9=0的图像的主要步骤。

根式复合函数y=√(x^2+3)的图像示意图,本经验通过函数的定义域、单调性、凸凹性、极限等，介绍函数的图像的主要步骤。

三维不等式柯西定理应用举例详解A15,本文介绍三维不等式柯西定理及其证明，并通过四个例子来详细说明该不等式的数学实际应用。

不定积分70x³/√32-39x²的计算过程,本文根据分部积分法、三角换元法以及凑分法等方法，介绍不定积分I=∫70x³/√32-39x²dx的计算步骤。

求函数y=5x6+9x+arcsin5：x的导数计算步骤,本文主要通过函数和求导规则，介绍函数y=5x^6+9x+arci5：x的一阶、二阶和三阶导数计算步骤。

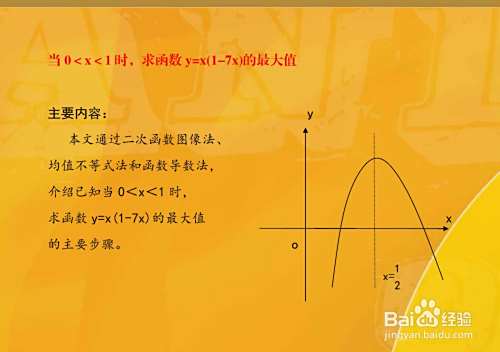
当0＜x＜1时，如何求函数y=x(1-7x)的最大值,本文通过二次函数图像法、均值不等式法和函数导数法，介绍已知当0＜x＜1时，求函数y=x1-7x的最大值的主要步骤。

函数y=(8x^n+cosx^2)^3的导数计算及对比分析,本文通过函数的链式求导和取对数求导方法，介绍多种函数构成复合函数y=8x+cox^2^3的导数计算主要步骤。

七个集合{3,6,9,12,15,18,21}的子集列举,本经验通过列举方法，介绍七个元素集合{3,6,9,12,15,18,21}集合的所有子集。

中考数学两点间距离最小值计算应用解析(16),根据两点的特征，即是否含有参数及参数数量，介绍计算两点间距离最小值的计算过程与步骤。

导数工具画y(x^2+20)√(x^2+18)=88图像示意图,介绍函数yx^2+20√x^2+18=88的定义域、值域、单调性及极限等性质，同时简要画出函数yx^2+20√x^2+18=88的图像示意图。

根式函数y√(4x+4)=√(4x-5)的性质归纳解析,本经验主要介绍函数y√4x+4=√4x-5的定义域、值域、单调性、凸凹性等性质。

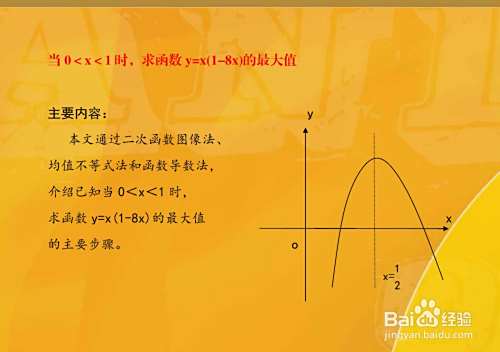
0＜x＜1时，求函数y=x(1-8x)的最大值的几种方法,本文通过二次函数图像法、均值不等式法和函数导数法，介绍已知当0＜x＜1时，求函数y=x1-8x的最大值的主要步骤。